课程地址
光栅化
Pixel:picture element
由三个红蓝绿三个颜色组成
屏幕空间
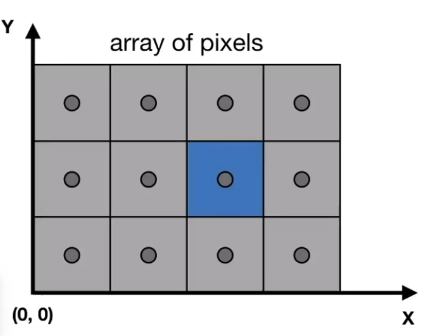
像素的坐标如上图由(x,y)组成;
像素的坐标取值在(0,0)到(width-1,height-1)之间;
像素的中心在(x+0.5,y+0.5);
屏幕覆盖范围(0,0)到(width,height)
视口变换
Canonical Cube to Screen(投影得到的标准立方体到屏幕空间的变换)
将xy平面[-1,1]2转换到[0,width]×[0,height]
转换矩阵如下: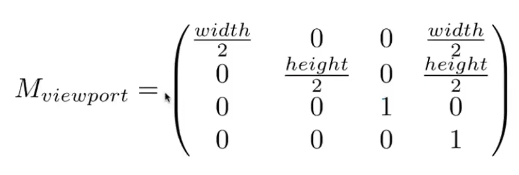
Drawing to Raster Device
为什么使用三角形:
- 三角形是基础多边形;
- 其他多边形可以拆成三角形;
- 三角形一定是平面;
- 可以很容易定义内部和外部;
- 可以根据三个顶点的关系,在三角形内部进行插值,以得到渐变的值。
判断像素与三角形的位置关系:
- 采样:利用像素中心对屏幕空间进行采样,判断像素中心是否在三角形内
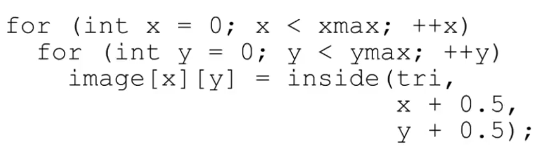
- inside(tri,x,y)函数:
三次叉乘,叉乘可以判断一个向量在另一个向量的左侧或右侧,(这里必须保证三角形的绕序) - 加速光栅化:
使用轴向包围盒(AABB):
包围盒外的不需要进行判断,包围盒内的执行之前的循环。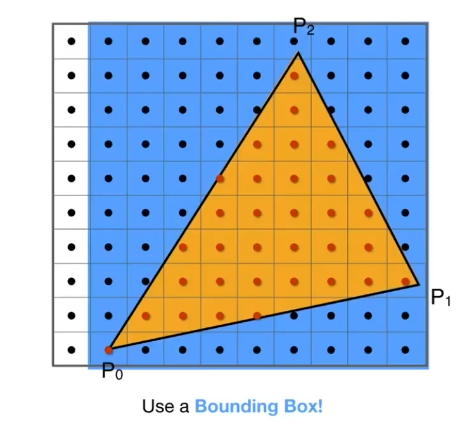
Increment Triangle Traversal:
判断每一行的最左和最右,只判断里面的点。
Antialiasing(反走样)
Antialiasing
Sampling Artifacts:采样出现的视觉错误,比如锯齿、摩尔纹等。
Antialiasing Idea:在采样前,先对图像进行模糊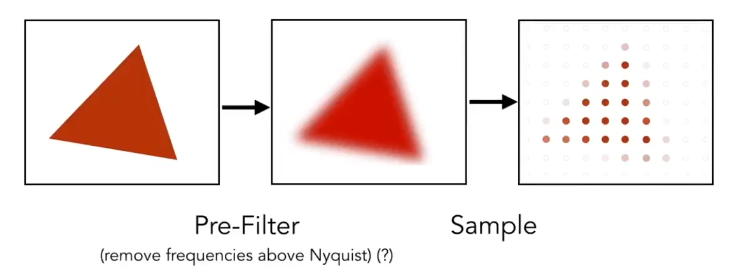
频域分析
傅里叶级数展开:任何一个周期函数可以写成一系列正弦和余弦函数的组合表示
傅里叶变换: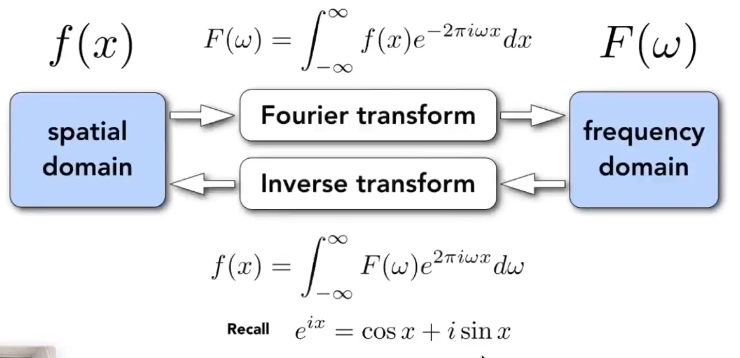
高频率函数需要更高频率的采样: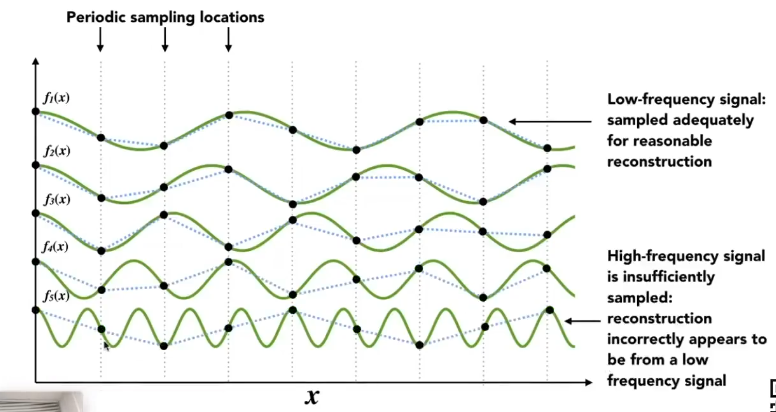
Aliases:同样的采样方法采样两种频率截然不同的函数,其采样结果却相同,这种现象被称之为走样。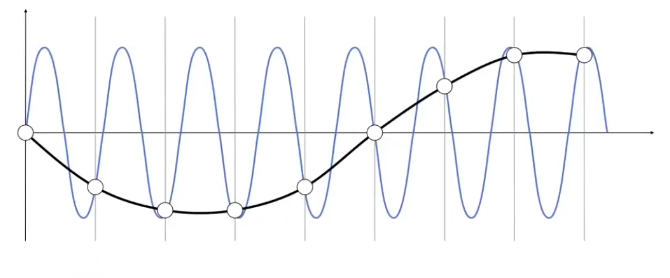
滤波
原图:
高通滤波:高频信号代表边界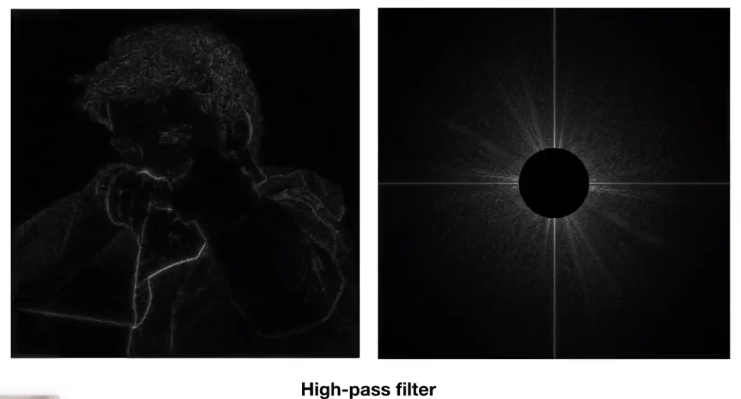
低通滤波:模糊处理
同时去掉高频和低频信息
滤波=平均=卷积
卷积: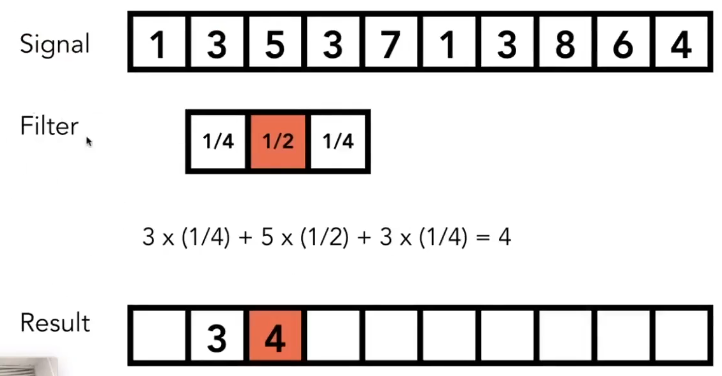
时域上两个信号的卷积,是两个信号在频域上的乘积;时域上两个信号的乘积,是两个信号在频域上的卷积。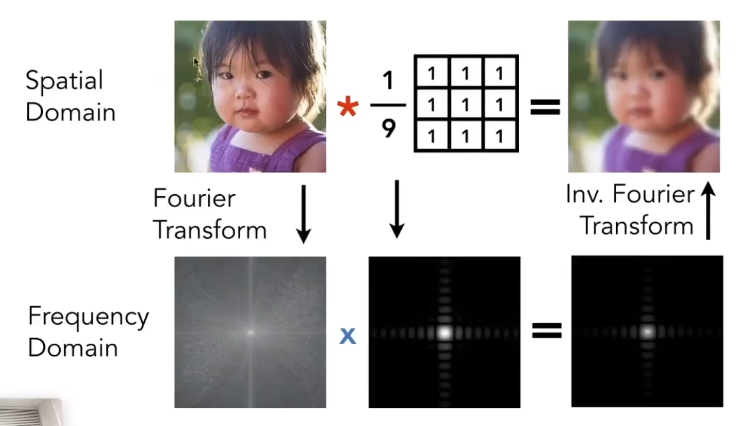
采样
采样 = 复制频谱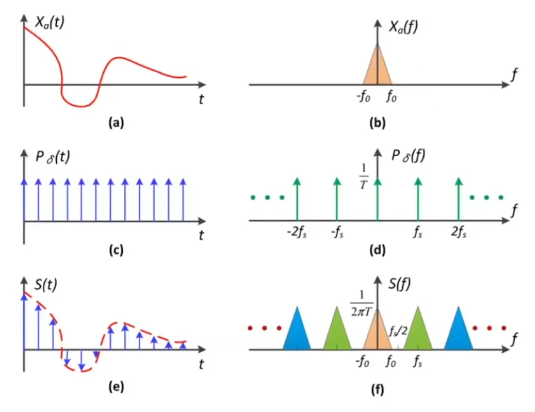
走样 = 频谱的混叠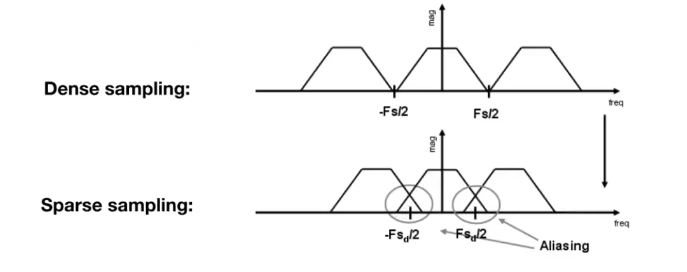
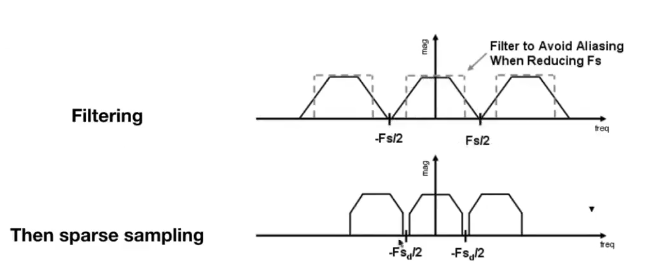
去除走样的方法:
- 增加采样率
- 反走样:先做模糊(低通滤波),再做采样
对每一个像素覆盖的区域的颜色求一个平均值(低通滤波)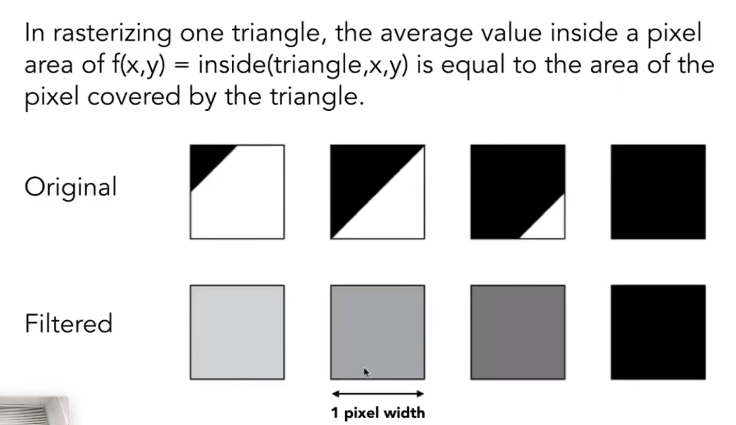
Multi-Sample Antialiasing(MSAA)
假设一个像素被划分为若干个子像素,并对子像素的值进行平均。
缺点:计算量增加。
其他反走样技术
FXAA(Fast Approximate AA):一种后处理方法,找到图像的锯齿位置,并去掉
TAA(Temporal AA):复用上一帧的结果
Super resolution/super sampling
将低分辨率的图拉大成高分辨率的图,且需要避免锯齿
DLSS(Deep Learning Super Sampling):利用深度学习猜缺失的细节