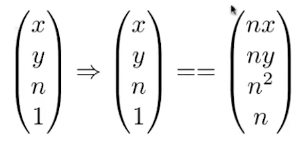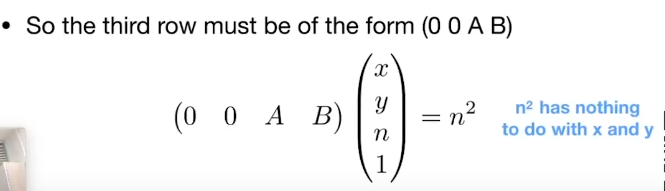课程地址
二维变换
Scale
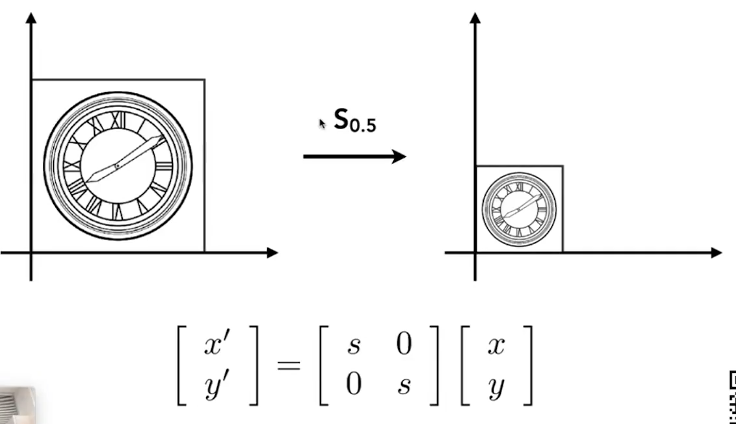
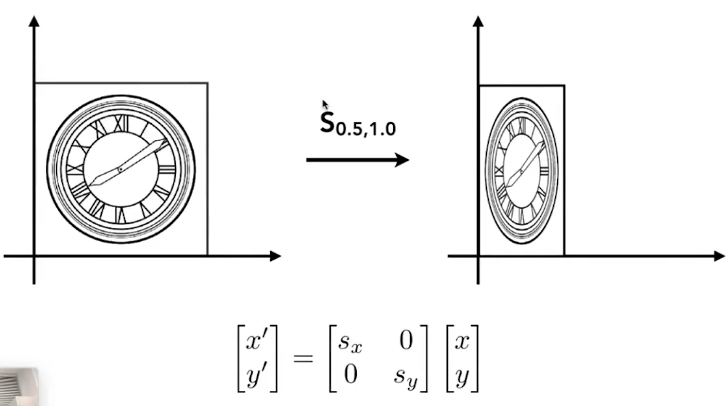
此外,如果要沿y轴翻转,则sx=-1,sy=1即可,沿x轴翻转同理
Shear(切变)
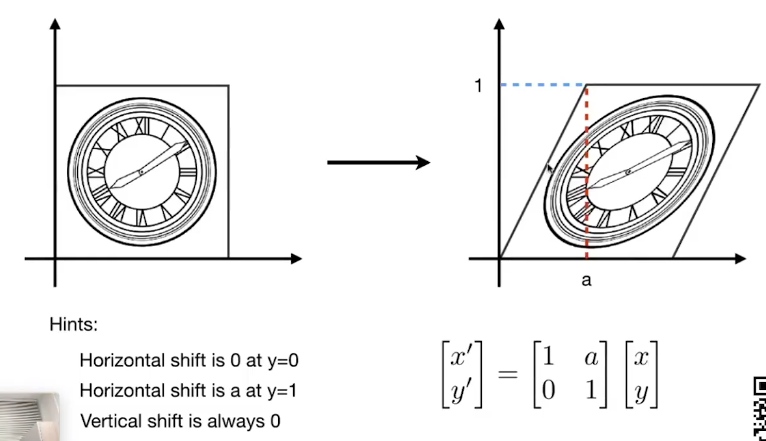
如果要计算变换矩阵,只需找到变换前后点的对应关系,再将其转换成矩阵表示即可。
Rotate(以原点为中心,逆时针)
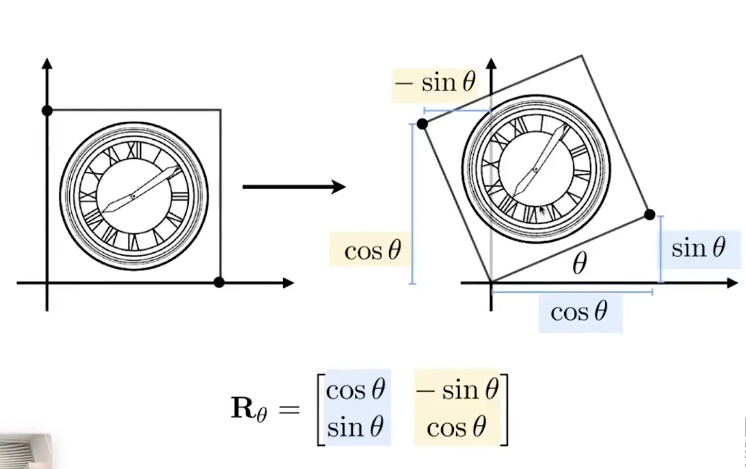
Linear Transformation
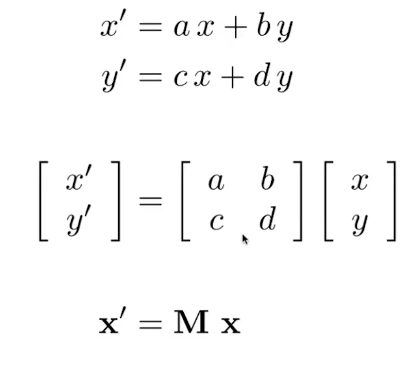
Translation
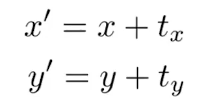
然而上式无法转换为二维的变换矩阵
只能写成如下的形式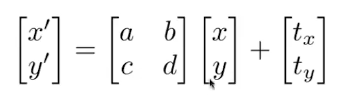
因此需要引入齐次坐标,以便于将所有变换写成统一的形式
Homogeneous Coordinator

由于向量不需要平移变换,因此向量的第三个数为0,且分别对待点和向量可以保证如下性质。
齐次坐标具有下面性质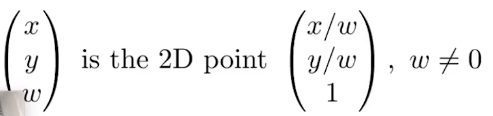
因此,点加点表示两个点的中点
齐次坐标表示仿射变换(先线性变换,在平移):
各种变换的齐次坐标变换表示:
Inverse Transform:
即乘以这个变换的逆矩阵,其意义是该变换的逆变换
需要注意
变换的顺序十分重要,否则可能无法得到想要的结果。
此外,矩阵的应用顺序是从右到左,即最右边的矩阵是第一个变换
变换的合成: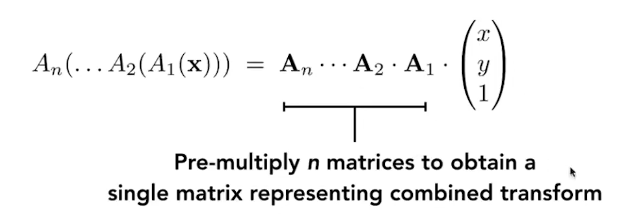
可以先将所有的变换相乘为一个矩阵,再对所有点进行变换。
变换的分解:
加入以点c为中心进行旋转,则如下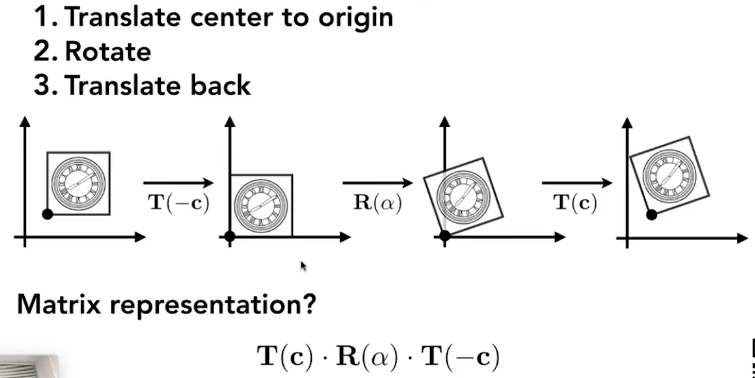
三维变换
三维的齐次坐标与二维的类似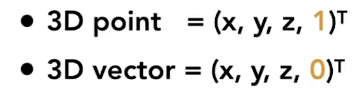
其他变换的齐次坐标表示均与二维情况类似,但需要额外考虑z轴。
三维Rotate
其中需要注意的是旋转操作,以x、y、z轴旋转的矩阵分别如下:

其中绕y轴的旋转有所不同,可以考虑右手螺旋定则以解释。
给定旋转轴n和旋转角$\alpha$,默认以原点为起点,所得出的旋转矩阵如下: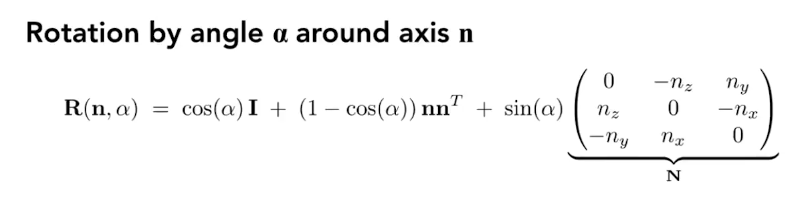
四元数也可以用于表示旋转(视频中没有提到具体内容)
View/Camera Transformation
model transformation: 模型自己的变换
View transformation: 相机位置的变换
projection transformation: 投影平面上
相机的三个属性: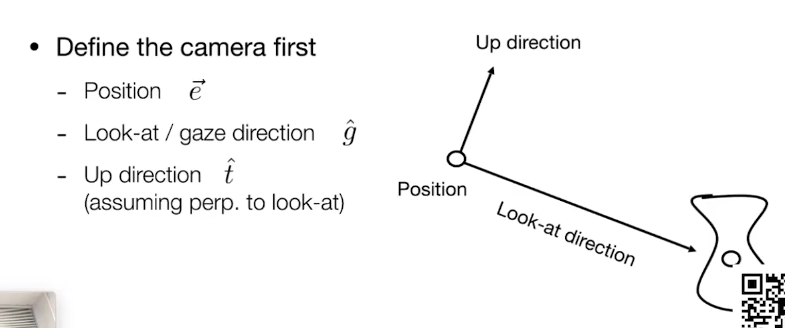
View transformation: 将相机移到原点,向上方向为y轴正方向,看向z轴负方向,所有物体按照相机的变换方式进行变换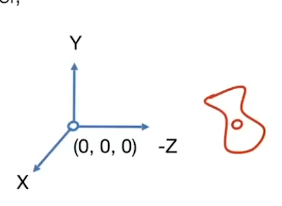
变换的方式如下

Projection Transformation
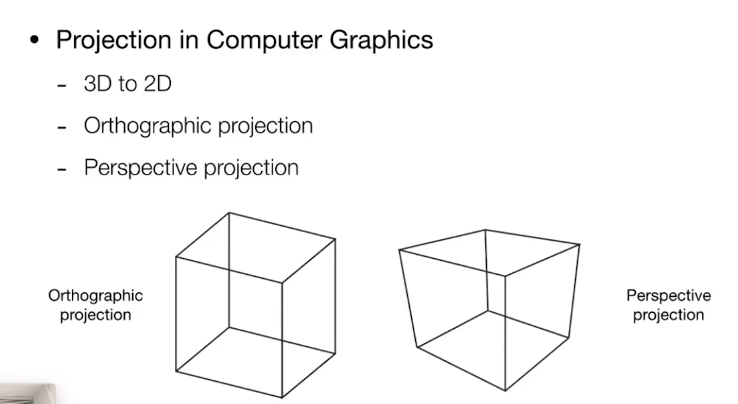
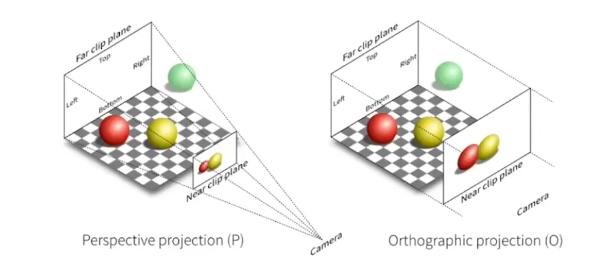
Orthographic Projection
只需要去掉z的值,并将结果放倒[-1,1]2的矩形上,就是正交投影
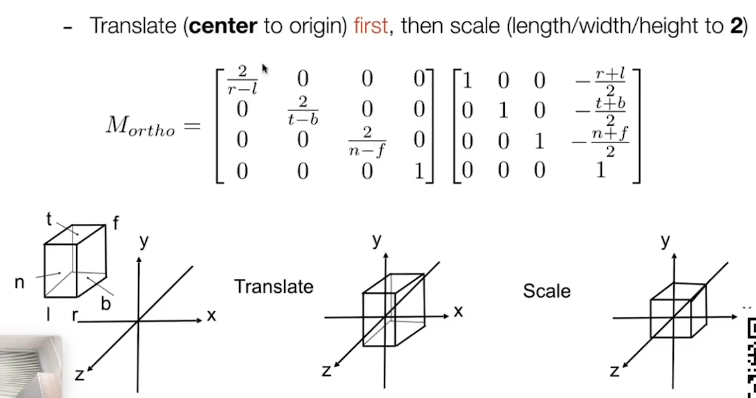
归一化的长方体可以理解为显示区域
Perspective Projection
回顾齐次坐标的性质:
透视变换: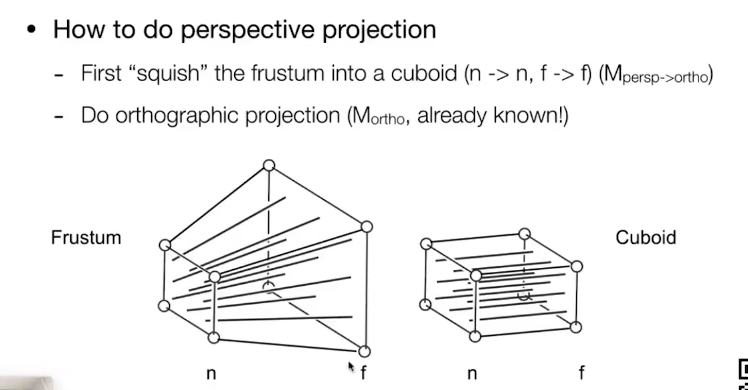
先将远平面挤成近平面,然后再做正交投影
如何挤压: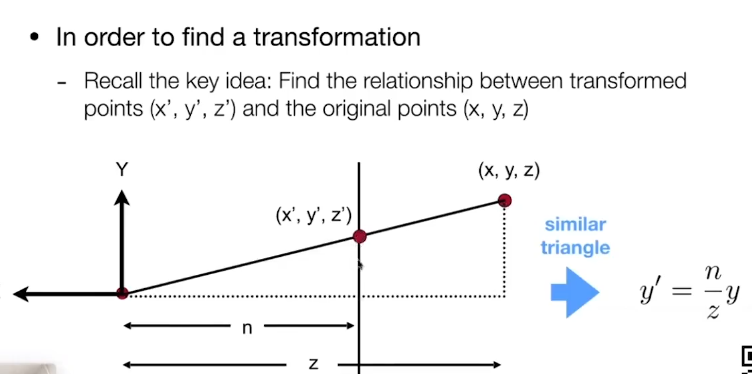
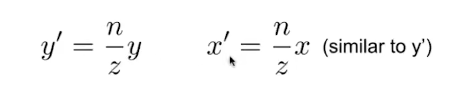
挤压时齐次坐标的变换方式:
假设变换后的近平面和远平面的z值不变,则有