原文链接
The Reyes image rendering architecture
前言
我是这两天才得知今年的图灵奖被授予给了两位图形学界的大佬,看了他们的事迹后,感觉激动得说不出话,今天就让我们回顾一下其中一名图灵奖得主Edwin E. Catmull所参与的关于图形管线的论文,这篇论文中所提出的图形管线中的核心思路被沿用至今。
论文要解决的问题
模型复杂性:由于之前无论多复杂的渲染图像相比于真实画面都显得过于简单,这是由于真实画面包含丰富的图形和纹理。为实现画面的真实感,需要数十万个几何图元。
模型多样性:包括图元、分形、粒子系统等
着色复杂性:由于表面反射特性过于复杂,因此需要一个可编程的着色器。
最小化光线追踪:许多非局部光照效果都可以用纹理映射来近似。在自然场景中,只有少数物体需要光线追踪。
速度:动画渲染需要严格的速度需求。
画面质量:需要保证画面质量,避免锯齿等错误。
灵活性:架构需要灵活兼容新的技术。
设计原则
自然坐标系:每种计算都需要一个坐标系系统以自然地进行这种计算。比如纹理映射需要使用uv坐标系,可视表面计算需要屏幕空间坐标系等。
向量化:架构应该利用向量化、并行化和管线,相似的计算应该一起进行,比如对于同一画面的计算通常是相似的,因此需要同时进行着色。
同一表示:许多算法只能处理简单的几何形状,因此需要将几何图元转换为多个微多边形表示的近似,所有的着色计算和可视化计算都在微多边形上进行。
局部性:
- 几何局部性:每个几何图元的计算不应该依赖于其他几何图元,并且每一个几何图元只能计算一次。
- 纹理局部性:只有当前需要的纹理在内存中,纹理应该中从磁盘中读取一次。
线性关系:渲染时间应该与模型的大小成线性关系
大模型:模型不应限制几何图元的数量
后门:架构中应该有”后门”,以便于其他程序可以被用来渲染一些物体。
纹理贴图:纹理贴图的访问应该是有效的,本文期望每个surface可以使用几个纹理。此外,纹理是定义复杂着色性质的强有力的工具。
设计细节
几何局部性
当光线追踪反射或折射任意表面时,都有可能产生次级光线。虽然这些次级光线命中的物体可以很快被计算出来,但是必须从数据库中访问该对象。随着模型越来越复杂,访问这些模型的开销会越来越大,因此光线追踪不适合渲染极度复杂的环境。
使用纹理贴图可以近似这些非局部计算,比如反射、折射和阴影的纹理贴图可以很好地近似这些效果,并且可以避免大量的访存和计算。
点采样
点采样具有简单,功能强大,并能够简单地适用于不同类型的图元。但是,采样可能会导致失真。因此本文采用蒙特卡洛方法(随机采样)。
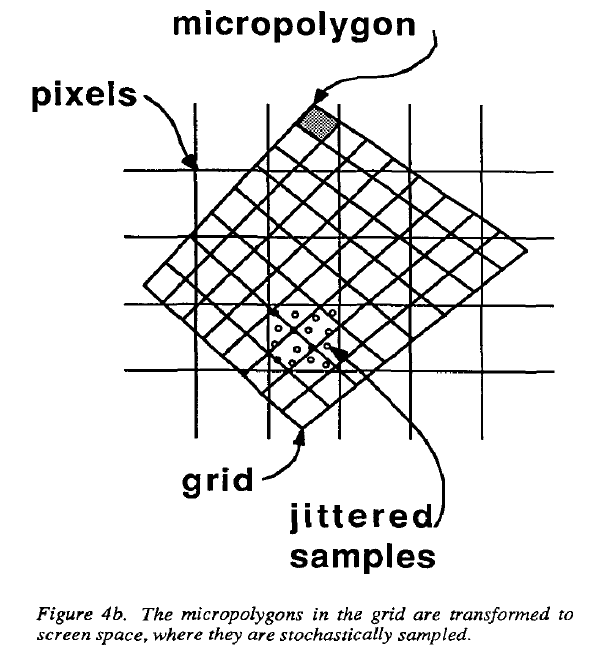
本文采用一种名为jittering的随机采样方法,像素被分为多个子像素,每一个子像素有一个采样点,这个采样点的位置就由jittering决定。该方法被用于采样为多边形覆盖的子像素。屏幕中每个采样点的当前可见性信息被存在z-buffer中。
微多边形
微多边形是算法的几何基本单元,是平面可着色的四边形,其中的每一条边约为1/2的像素。这是因为半个像素是一个图像的奈奎斯特极限,表面着色可以被每个微多边形的单一颜色充分表示。
将几何图元划分为微多边形的过程被称为dicing,其结果是一个二维微多边形数组,被称为grid。此外,由于相邻微多边形的共享顶点只被表示一次,因此grid中的微多边形需要更少的存储。
dicing在eye space空间中实现,并根据屏幕中图元大小的估计值进行dice,即需要创建多少个微多边形。
使用微多边形并被着色具有以下几个优势:
- 向量化着色:如果每一个点的着色计算操作相似,则着色操作可以被向量化(这里可能是并行化的意思)
- 纹理局部性:通过按顺序访问大型连续纹理块进行纹理请求,因为着色可以按物体顺序执行,避免了其他算法中发生的纹理颠簸(即需要反复从磁盘中读取相同的纹理)。比如当纹理请求分成小块且在不同的几种纹理贴图间切换时,就会发生纹理颠簸。
- 纹理过滤
- 细分一致性:由于可以一次对整个表面进行细分,因此可以通过正向差分等有效技术细分。
- 裁剪:不需要像某些算法所要求那样需要沿着像素边界裁剪对象
- 位移贴图类似于凹凸贴图,表面的位置和其法向量会发生改变,这使得纹理贴图称为建模表面或者存储建模程序结果的一种手段。由于位移贴图可以改变表面位置,因此必须在隐藏表面(应该是深度检测)计算之前计算。
- 不需要进行透视畸变矫正:由于微多边形比较小,因此不需要对插值的透视畸变进行矫正。
纹理局部性
假设,s、t表示纹理贴图上的坐标,u、v表示一个surface上的纹理参数坐标。
纹理通常被划分为两类:一致性访问纹理(CATs)和随机访问纹理(RATs)。对于一致性访问纹理来说s=au+b,t=cv+d,其中a、b、c、d分别为常数。其他的纹理均为RATs。
此外,CATs相比于RATs处理更容易且速度更快,因为如果通过uv的顺序进行着色计算,则可以顺序地访问纹理贴图。
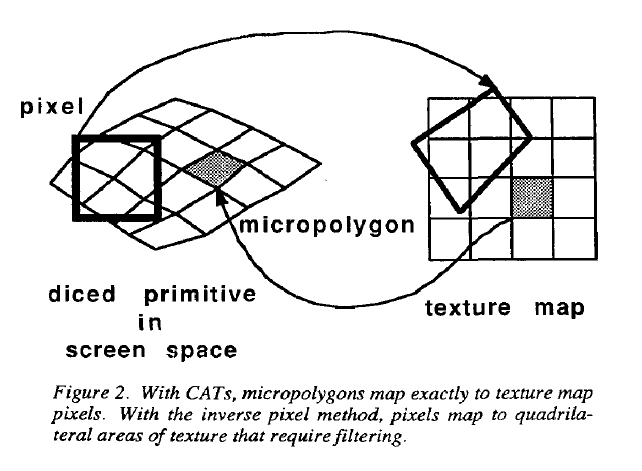
RATs比CATs更加通用,比如,环境贴图是RATs,因为根据反射的方向进行索引。再比如,decal,即世界空间上纹理在surface上的平行投影,其中s、t依赖于x、y、z,而不是u、v。
算法描述

下面将讨论上述算法所用到的几个过程:
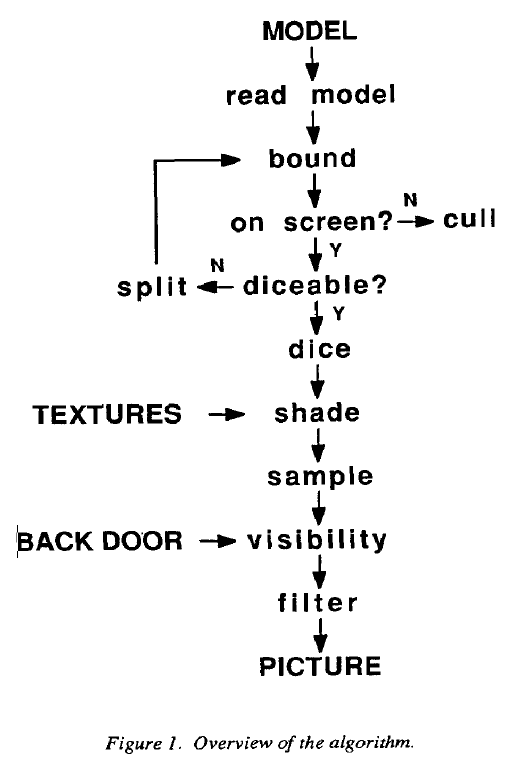
Bound:图元可以计算它的视角空间的bound,屏幕空间的bound由视角空间转换而来,图元必须在其bound内,但这个bound不一定是紧的。
Dice:不是所有类型的图元需要是diceable的,唯一的要求是每一个图元可以能够将自己split成其他图元,这种split最终可以让图元完全被dice。
split:图元能够将自己split成一个或多个相同类型或其他类型的图元。
Diceable test:这个测试决定图元是否应该被dice或split。如果一个图元被分割后将产生太多的微多边形或特别大的微多边形,则这个图元被认为是not diceable的。

如果一个物体完全视椎体外,则被剔除; 如果一部分在视椎体外一部分在视椎体内则依旧被保留、着色和采样。只有在视椎体内的区域才有可能被采样。
有时物体一部分在眼睛后面,但另一部分在视椎体内。其处理过程如下图:
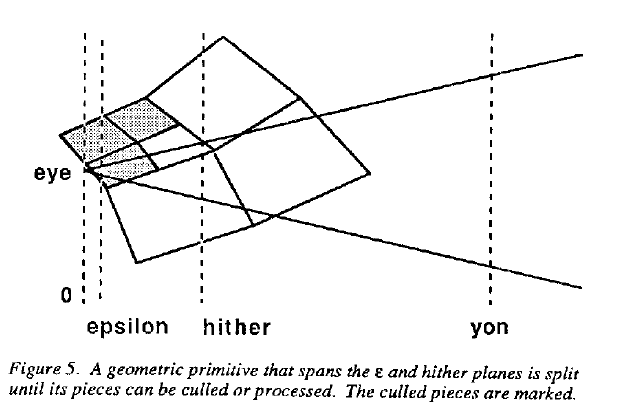
实现方式
由于当时的内存不够大,但z-buffer需要大量的内存,因此屏幕被分为rectangular buckets,这些bucket被放在内存或者磁盘中。在初始的过程中,检测每一个图元的边界,并将对应其放入对应的bucket中,在剩下的计算中,按需对桶bucket进行处理。首先,对bucket中的图元进行split或者dice。当图元被dice后,其微多边形被着色,并放入其覆盖的bucket中。当bucket中的所有图元被split或diced后,这个bucket中的微多边形被采样。因此,只需要一个bucket对应屏幕大小的z-buffer即可。
总结
本文所提的图形管线的一些设计原则和设计思路被沿用至今。
由于本文部分内容的表达方式可能与现在的表达方式有所出入,如果本篇分享存在问题,欢迎提出。